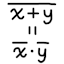Boolean algebra laws
Notation
The following notation is used for Boolean algebra on this page, which is the electrical engineering notation:
- False: 0
- True: 1
- NOT x: x
- x AND y: x · y
- x OR y: x + y
- x XOR y: x ⊕ y
The precedence from high to low is AND, XOR, OR. Examples:
- x + y · z means x + (y · z)
- x ⊕ y · z means x ⊕ (y · z)
- x + y ⊕ z means x + (y ⊕ z)
Basic laws
Constants
- NOT:
- 0 = 1
- 1 = 0
- AND:
- 0 · 0 = 0
- 0 · 1 = 0
- 1 · 0 = 0
- 1 · 1 = 1
- OR:
- 0 + 0 = 0
- 0 + 1 = 1
- 1 + 0 = 1
- 1 + 1 = 1
- XOR:
- 0 ⊕ 0 = 0
- 0 ⊕ 1 = 1
- 1 ⊕ 0 = 1
- 1 ⊕ 1 = 0
Constant and variable
- AND:
- 0 · x = 0
- 1 · x = x
- OR:
- 0 + x = x
- 1 + x = 1
- XOR:
- 0 ⊕ x = x
- 1 ⊕ x = x
One variable
- NOT:
- NOT x = x
- AND:
- x · x = x
- x · x = 0
- OR:
- x + x = x
- x + x = 1
- XOR:
- x ⊕ x = 0
- x ⊕ x = 1
XOR
XOR can be defined in terms of AND, OR, NOT:
- x ⊕ y = (x · y) + (x · y)
- x ⊕ y = (x + y) · (x + y)
- x ⊕ y = (x + y) · (x · y)
Commutativity
- AND: x · y = y · x
- OR: x + y = y + x
- XOR: x ⊕ y = y ⊕ x
Associativity
- AND: (x · y) · z = x · (y · z)
- OR: (x + y) + z = x + (y + z)
- XOR: (x ⊕ y) ⊕ z = x ⊕ (y ⊕ z)
Distributivity
- x · (y + z) = (x · y) + (x · z)
- x + (y · z) = (x + y) · (x + z)
- x · (y ⊕ z) = (x · y) ⊕ (x · z)
De Morgan’s laws
- NAND: x · y = x + y
- NOR: x + y = x · y
Redundancy laws
The following laws will be proved with the basic laws. Counter-intuitively, it is sometimes necessary to complicate the formula before simplifying it.
Absorption
- x + x · y = x
-
Proof:
x + x · y
= x · 1 + x · y
= x · (1 + y)
= x · 1
= x - x · (x + y) = x
-
Proof:
x · (x + y)
= (x + 0) · (x + y)
= x + (0 · y)
= x + 0
= x
No name
- x + x · y = x + y
-
Proof:
x + x · y
= (x + x) · (x + y)
= 1 · (x + y)
= x + y - x · (x + y) = x · y
-
Proof:
x · (x + y)
= x · x + x · y
= 0 + x · y
= x · y - x · y + x · y = x
-
Proof:
x · y + x · y
= x · (y + y)
= x · 1
= x - (x + y) · (x + y) = x
-
Proof:
(x + y) · (x + y)
= x + (y · y)
= x + 0
= x
Consensus
- x · y + x · z + y · z = x · y + x · z
-
Proof:
x · y + x · z + y · z
= x · y + x · z + 1 · y · z
= x · y + x · z + (x + x) · y · z
= x · y + x · z + x · y · z + x · y · z
= x · y + x · y · z + x · z + x · y · z
= x · y · 1 + x · y · z + x · 1 · z + x · y · z
= x · y · (1 + z) + x · z · (1 + y)
= x · y · 1 + x · z · 1
= x · y + x · z - (x + y) · (x + z) · (y + z) = (x + y) · (x + z)
-
Proof:
(x + y) · (x + z) · (y + z)
= (x + y) · (x + z) · (0 + y + z)
= (x + y) · (x + z) · (x · x + y + z)
= (x + y) · (x + z) · (x + y + z) · (x + y + z)
= (x + y) · (x + y + z) · (x + z) · (x + y + z)
= (x + y + 0) · (x + y + z) · (x + 0 + z) · (x + y + z)
= (x + y + 0 · z) · (x + z + 0 · y)
= (x + y + 0) · (x + z + 0)
= (x + y) · (x + z)
